Semi di Scienza (Seeds of Science) is an Italian cultural association devoted to high quality outreach activities with the aim of bringing science closer to the general public. They are doing an amazing work collaborating with researchers who write for them on the most diverse research topics but also organizing events in schools, “Outreach Dinners” and “Scientific Happy Hours”…
I was extremely happy when Semi di Scienza, asked me if I was interested in writing a post on their blog about my research. I accepted immediately! The topic was free and I chose to write on instabilities, in particular on instabilities of light. It is quite difficult to explain a technical topic in a few lines but I did my best also trying to highlight the potential of instabilities for applications!
The post is now online and italian speaking web surfers can have a look at it here. Anyway I translated it into English too: “Instabilities of light: why they matter”. Enjoy!
Instabilities of light: why they matter
We are frequently used to consider instabilities as negative facts: economical instability, mental instability, geopolitical instability: we don’t think of them as desirable situations. Let alone instabilities of engineering works, like for instance a house, a palace, a bridge, the instability of a computer program, and what about the one of a plane wing? We consider those objects as being able to accomplish the function for which they have been made exactly because of their robustness and because of their stability with respect to undesired influence manifesting itself independently of our control. We strongly wish that perturbations acting on the object from outside will be damped and in a certain way neutralised, avoiding that its functionalities would be jeopardised, or even worse that our bridge, our house or whatever other object will be destroyed. The same things could be thought of a light source, which has been designed for a precise purpose; we would wish that its emission intensity does not substantially fluctuate in time, neither that it drastically changes with the smallest variation of the temperature, of the electric voltage nor with sound vibrations due to people voices or noise in the room. It would seem that, in general, instabilities of mechanical systems, or even of social structures (given that they are working well and efficiently) could be an undesirable situation.
Since more than a century, instabilities have been the object of scientists interest, who studied them in many different situations: in fluids, in plasmas, in mechanical systems of various kinds, and in biological, chemical and optical systems too. Basically every system in nature is subject to various kinds of perturbations caused by the surrounding environment, and these perturbations, if they are amplified could lead to the instability of the original state of the particular system concerned, causing dramatic qualitative changes. The study of instabilities is of great interest, and instabilities are believed to constitute the basis of countless important phenomena, as for instance the formation of freak waves in oceans just to make one example.
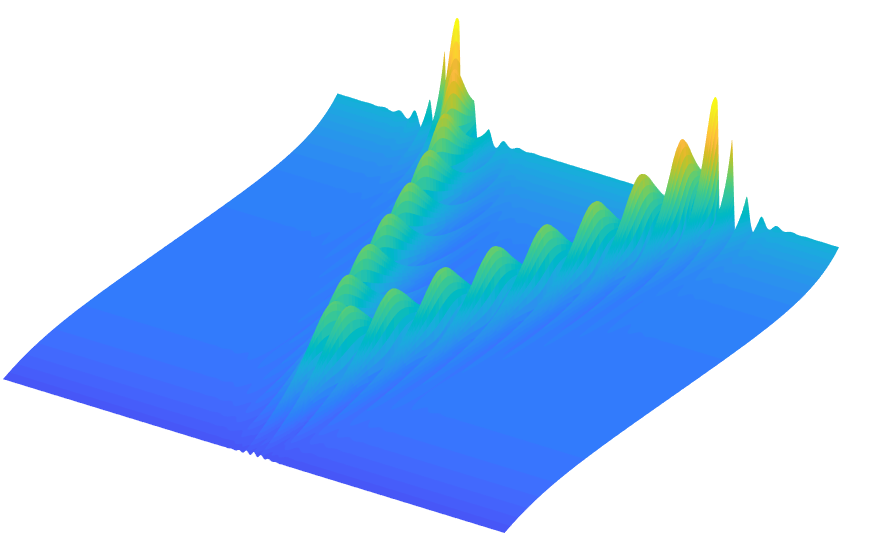
I would like now to briefly describe, some peculiar situations, where the context in which the fact that an instability manifest itself is desirable and not to be avoided: situations in which stability is surprisingly an obstacle to the development of technologically useful functionalities. I will pursue this goal by presenting a couple of simple examples taken from the physics of nonlinear optics. Before starting, it is important to make a clarification: while it is crystal clear that optics is the science which studies light phenomena, the meaning of the expression “nonlinear” could be much more obscure to a non technical audience. The elucidation of the meaning of “nonlinear” in this context would definitely require a dedicated detailed in-depth analysis. For the purpose of this post, it is enough to say that a nonlinear material medium has a response proportional to the second, third or higher powers of the amplitude of the light wave propagating through it. A linear medium instead has a response which is simply proportional to the light wave amplitude itself. Nonlinearity is at the heart of new light frequencies generation, of lasers operational principle and of other fascinating phenomena. Generally speaking nonlinear effects are weak and require substantial light intensity to appear, but when they manifest themselves, they open the door to new and unexpected dynamics. Let us now come back to the point. The first example is the following: Let us consider a light wave, which propagates along an optical fibre. An optical fibre is a small “pipe” made out of a peculiar glass, having a diameter smaller than a millimetre, which guides the light, by keeping it confined due to the phenomenon of total internal reflection, allowing its propagation for distances ranging from several tens to several hundreds kilometres. Basically a dense net of interconnected optical fibres, on earth and under the oceans, constitutes the backbone of the whole internet infrastructure. Let us consider for the moment, instead of fibres used for optical telecommunications, which are several tens of kilometres long, a fibre whose length is about few tens of metres, and at one end of such fibre, let us inject a light wave with a single frequency, a single colour (although in general the electromagnetic radiation used is located in the near infrared region of the spectrum). If the fibre has certain properties (in technical jargon we say that the fibre has anomalous chromatic dispersion, which means that light waves oscillating with larger frequency travel faster than those ones with lower frequency) and if the power of the injected wave is sufficiently high, then the light wave that we will observe at the output of the fibre will exhibit, due to the fibre nonlinearity, new properties which qualitatively differ from the ones at the input. The amplitude of the wave at the fibre output is not constant anymore, but on the contrary it presents substantial variations which could be either periodic and regular but also irregular depending on the particular conditions in which the process unfolds. The original input wave is unstable, small perturbations, wavelets which at the input of the fibre had irrelevant amplitude, have grown substantially subtracting energy from the primary wave up to the point of qualitatively modifying its shape. This process is called modulation instability. This phenomenon is enabled by the nonlinear response of the fibre!
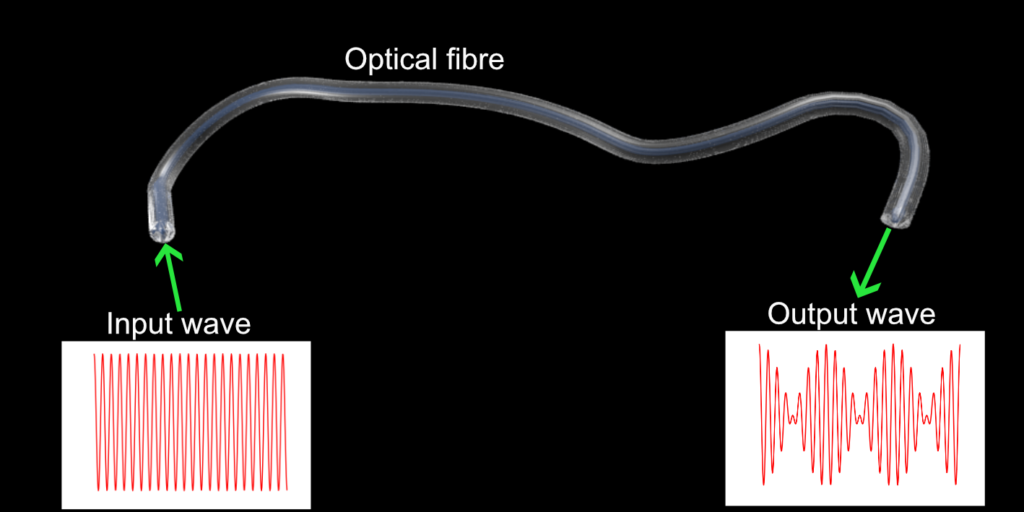
Now one could think that this instability process is detrimental for the correct operation of a device which requires that the travelling light wave remains unchanged. This one is definitely a well motivated objection. But, let us look at the situation from another perspective: if the primary input wave loses energy, the perturbations (waves oscillating at different frequencies) gain such energy. This is the resource we can exploit! Mathematical analysis allows us to calculate how much energy is gained by the small waves (the instability gain), as a function of the fibre and primary wave parameters, at least in the initial stage of their amplification. But how can we make use of this gain for the small amplitude waves? If, instead of letting that arbitrary waves, initiated by quantum vacuum fluctuations or by optical noise, are amplified during the instability process; we can inject ourselves, at the fibre input besides the primary wave (also called the pump wave), other waves of different frequencies and low energy that we want to amplify. Ideal candidates are the optical signals which are used to carry information. They will constitute the “seed”, from which the primary wave instability will develop, absorbing part of its energy and emerging with amplified amplitude at the fibre output.
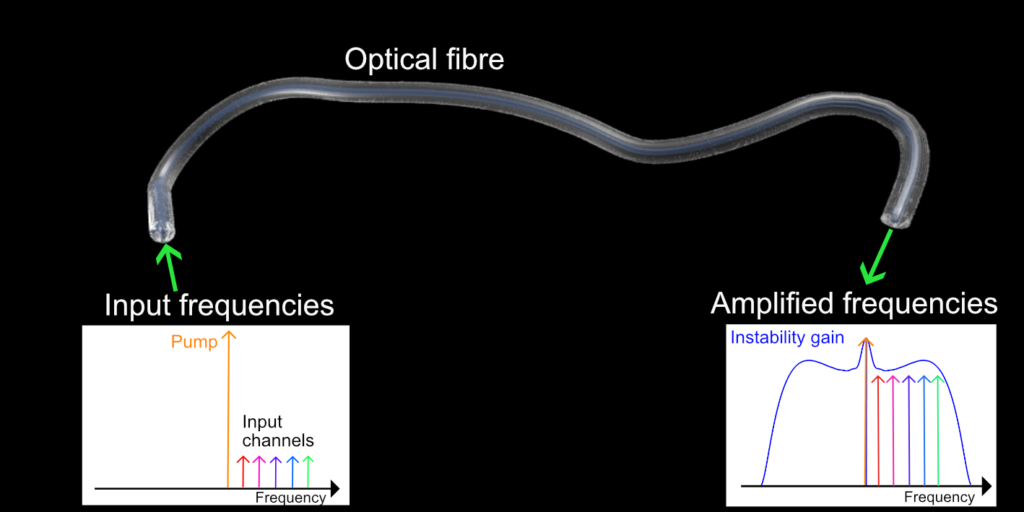
Optical signals used in fibre optics telecommunications consist indeed of many “channels”, each one corresponding to a different frequency, propagating along fibres which allow parallel information transmission. The increasing demand of more information to be transmitted in fibre, due to the growing internet use in modern interconnected societies, requires to add more and more channels (new frequencies). This fact however causes an increase of the total frequency band occupied by signals: the bandwidth increase is unavoidable due to the fact that at present it is not possible to send signals too closely packed in frequency reducing the spacing between channels. Due to energy losses suffered by light propagating along optical fibres, a periodic signal amplification along the transmission line becomes necessary. Erbium doped fibre amplifiers whose invention has enabled the existence of internet in its present form, can amplify signals only in a limited frequency band. Researchers in this field are working hard to find alternative solutions. One of the most promising solutions is relying indeed on the modulation instability described above. Despite the fact of being in a research and development phase, still far from technological implementation, this solution has already enabled optical signals amplification allowing information transmission for thousands of kilometres. This new kind of amplifier is called fibre optical parametric amplifier. Hence, starting from a simple physical phenomenon entailing the instability of a light wave, a new technological concept has emerged which may have relevant impact in the society. Indeed researchers working in this field are now studying the conditions for engineering the instability in order to optimise its performances towards their goals: achieving a significant energy transfer homogenously distributed over a large frequency band. The paradigm of instability as a detrimental effect has been reversed.
Let us know turn to a second example. Another very interesting case of modulation instability is the one which takes place when single frequency light is injected in an optical microresonator, i.e. a tipically ring-shaped optical cavity made of silica or of semiconductor materials, where light is strongly confined and photons can circulate many thousands times before escaping. The great amount of energy stored corresponding to a light wave oscillating with a single frequency is such that, due to the nonlinear response of the material, an instability of the light wave itself is induced. The wave is destabilised via the amplification of other waves of different frequencies (different “colours”), which initially were simple perturbations of insignificant magnitude caused by quantum vacuum fluctuations or by optical noise present in the system. The primary wave amplitude is hence modulated by different waves, equally spaced in frequency, which are amplified: many cavity resonances are excited in this way. The light inside the cavity from monochromatic has become polychromatic. It is important to stress the fact that an optical cavity supports only oscillations which are integer multiple of a fundamental frequency, and hence the light waves which can resonate inside the cavities are equally spaced in frequency.
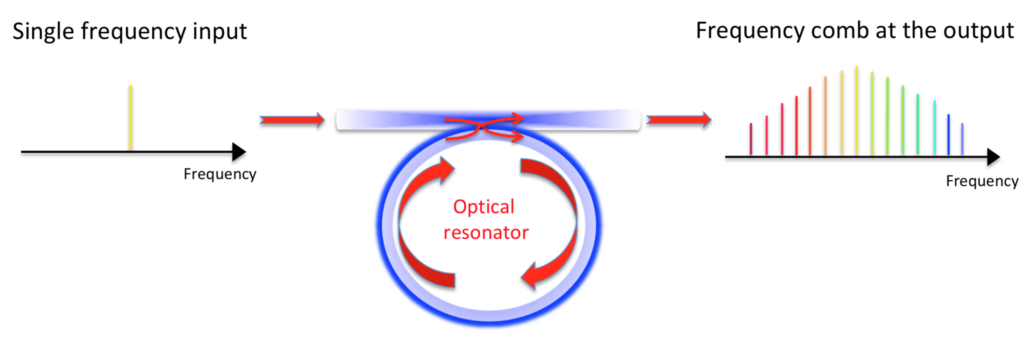
Due to the peculiar process involved in this instability, waves with different equally spaced frequencies oscillate in phase (respecting a certain synchrony): a light with this kind of spectrum is called a frequency comb. Frequency combs have remarkable applications they are currently used, and in a near future will be even more, in numerous contexts including precision spectroscopy, remote detection of greenhouse gases, exoplanets search (planets not belonging to our solar system), as optical clocks much more precise than existing atomic ones, and many more.
To conclude we can say that not every instability causes harm. Beyond their intrinsic scientific fascination instabilities are a precious and unexpected resource for the realisation of novel optical devices with important practical applications. Furthermore, the examples we have discussed show how research topics which apparently are purely academics, and whose study has been initially pursued for mere pleasure and scientific curiosity, can unexpectedly become materially useful for the whole society.