- Coffee House Post #1, Published online on 18th December 2019
- About the author: Dr. Stella Civelli, PhD in Emerging Digital Technologies & Photonic Technologies, is currently working at TeCIP Institute, Scuola Superiore Sant’Anna (Pisa, Italy) . Email address: [email protected] . You can find more details about her research and activities on: GoogleScholar, ResearchGate and www.semidiscienza.it .
- The research content of this post is mainly taken from: F. Da Ros, S. Civelli, S. Gaiarin, E.P.da Silva, N. De Renzis, M. Secondini, and D. Zibar “Dual-polarization NFDM transmission with continuous and discrete spectral modulation”, Journal of Lightwave Technology, Volume: 37, Issue: 10 (2019).
1. Introduction
The global data traffic grows exponentially every year, pushed by the ever-increasing use of web navigation, video streaming, and internet of things. Optical fibers are responsible for carrying the 99% of all this data around the globe, connecting cities and continents. The success of optical fiber communication started in the 80s thanks to the invention of the laser in the 60s, and the work of Kao in the 70s to develop fibers with sufficient low loss. Later, the advent of optical amplifiers, digital signal processing, wavelength division multiplexing, and higher order modulation formats, allowed to enormously increase the capacity of the optical fiber network and meet the increasing data rate demand [1,2].
Nowadays, the throughput of single mode fibers (SMF) is limited by the nonlinear Kerr effect, which imposes a severe limit in the use of higher signal-to-noise ratio (SNR) to increase the capacity of the network. Consequently, to avoid the forecasted and infamous “capacity crunch”, in the past years a significant research effort has been devoted to compensate and mitigate the nonlinear effects in optical fiber communications. While most of these techniques have developed starting from linear communication systems and treating the nonlinearity as a nuisance, a revolutionary approach that aims at mastering the nonlinearity has been investigated since 2014. This approach, currently known as nonlinear frequency-division multiplexing (NFDM), uses the inverse scattering transform (IST) to encode the information on some special degrees of freedom, the nonlinear frequencies, that propagate in optical fibers in a trivial manner (under some circumstances), despite the complicated and nonlinear evolution of the signal. While a preliminary version of NFDM was proposed in the pioneering paper of Hasegawa and Nyu in 1993 [3], it has been seriously investigated after the work of Yousefi and Kschichang [4] and the works from Aston University [5-6] in 2014—taking advantage of the additional degrees of freedom enabled by coherent communications.
2. State of the art
2.1. The nonlinear Fourier transform
The IST is a mathematical method to solve the initial value problem (IVP) associated to a certain class of nonlinear partial differential equations, referred to as integrable equation [7]. In a nutshell, the method consists in finding the solution of an associated linear ordinary differential equation (the scattering problem), describing the solution of the IVP. Finding the solution of the associated linear equation, will provide the solution of the IVP. In simpler words, the IST solves the IVP associated to the nonlinear partial differential equation moving to another domain—the nonlinear frequency domain—where the IVP is transformed to a simple linear equation. For its analogy to the standard linear Fourier transform, the IST has been re-branded as nonlinear Fourier transform (NFT) in the optical communication community. The history of the IST goes back to the 1834 when J. Scott Russel observed for the first time a solitary wave—a soliton—in water. A soliton is indeed a special solution of the IST that maintains its shape when propagating in time. Remarkably, the nonlinear Schroedinger equation (NLSE) and the Manakov equation—usually considered as master models for the propagation of a signal in a SMF, in the single and dual polarization case, respectively— are integrable with the NFT [7-8]. In the following, only these two equations will be considered. The Manakov equation can be considered as a two-dimensional generalization of the NLSE.
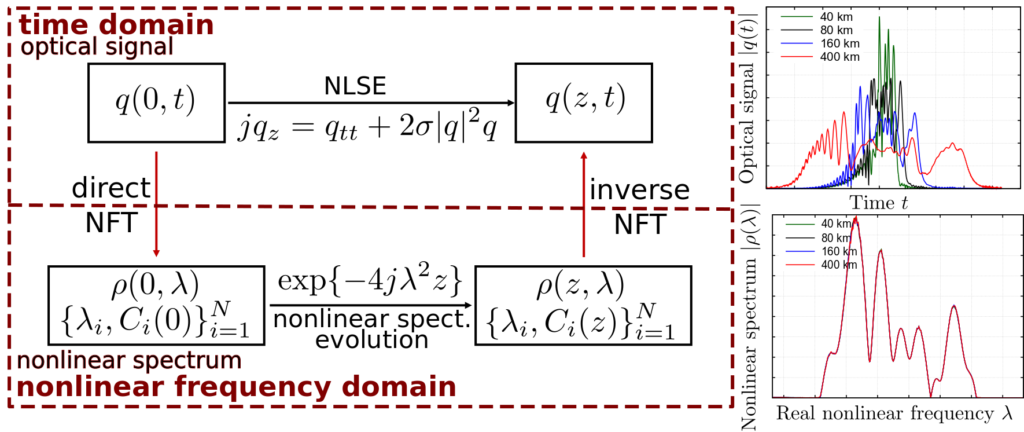
Figure 1: The NFT for the NLSE. The complicate evolution in space of the time domain signal (up) becomes trivial in the nonlinear frequency domain (down). An example of the time domain signal and its nonlinear spectrum at different distances is shown on the right. Figure adapted from [9].
The nonlinear spectrum of the optical signal is made of two parts. The continuous nonlinear spectrum is defined on real nonlinear frequencies and is a sort of nonlinear analogous of the standard spectrum. The discrete nonlinear spectrum is made of discrete points, defined on complex nonlinear frequencies and correspond to solitons. The propagation (in space) of these is given by the multiplication for an exponential factor [7].
The Figure 1 sketches the NFT scheme for the NLSE, showing the time domain in the upper part, and the nonlinear frequency domain in the lower part. The evolution in space is given by the NLSE in the first case and translates into a trivial operation in the second case. The direct and inverse NFT are used to go back and forth from the time domain to the nonlinear frequency domain. The right part of the figure shows the (modulus) of the signal (up) and the continuous nonlinear spectrum (down) at different propagation distances (noiseless and lossless scenario): the first is significantly subject to propagation effects, while the second remains unchanged.
2.2. Nonlinear frequency-division multiplexing
Given the indubitable strength of the NFT, it is reasonable to use it for communications using optical fibers. NFDM is the umbrella term for communication paradigms using the NFT for encoding and decoding information on the nonlinear spectrum [4-6,10]. Basically, the information is mapped on the nonlinear spectrum at the transmitter and an inverse NFT is used to obtain the signal to be launched into the fiber. At the receiver, the received time domain signal is used to perform a direct NFT and obtain the nonlinear spectrum propagated at the end of the fiber. Propagation effects are removed just multiplying for the inverse of the exponential factor, and the information sent can be finally retrieved.
NFDM is expected to outperform conventional systems for its inherent robustness against nonlinearity, allowing to encode different users on separated “bands of nonlinear frequencies”, thus avoiding any deterministic interference. For those who are familiar with fiber optic communication systems, NFDM is just the nonlinear analogous of the well know orthogonal frequency division multiplexing (OFDM), using the NFT rather that the Fourier transform.
Despite the simple working principle, many issues strongly affect the system and should be properly accounted for. Firstly, the mathematical theory of the NFT is very involved and affects (i) the development of efficient numerical algorithms for the direct and inverse NFT, required for the system implementation, and (ii) the derivation of theoretical-based optimal approaches for modulation and detection. Secondly, despite the fact that the NLSE (similarly the Manakov equation) is often considered as master model for the signal propagation in optical fibers, many other effects are not accounted for, e.g., amplification and noise. Unfortunately, NFDM is not exact anymore under these impairments, and their impact should be understood. Thirdly, due to the aforementioned issues, to facilitate the study, NFDM has been approached with techniques used for conventional systems. However, this approach may also simplify too much and worsens the impact of some impairments. A complete development (and, optimization) of the system in a nonlinear perspective should be considered.
For all these issues, the research about NFDM systems started considering a simplified scenario. For example, the modulation of a single polarization (considering the NLSE) rather than both (Manakov equation) was mostly investigated. Moreover, despite the fact that both nonlinear spectra (the continuous and the discrete) can be modulated, the modulation of these has been mostly investigated separately. In particular, the first experimental work with joint spectrum in single polarization dates back to 2017 [11], the first simulation-based work about discrete spectrum modulation for both polarization dates back to 2015 [12], and the first experimental work with dual polarization discrete spectrum modulation was done in [13].
As a matter of fact, our work “Dual-polarization NFDM transmission with continuous and discrete spectral modulation” published on the Journal of Lightwave technology in 2019 [14], and detailed in the following sections, was the first (and is still the only one) simulation-based and experimental demonstration of joint spectrum modulation on both polarizations.
3. Dual-polarization joint continuous and discrete NFDM
In this work, the information was encoded on both the continuous and the discrete spectra of the two polarizations of the optical signal. In particular, we encoded 16 QPSK symbols on each polarization of the continuous nonlinear spectrum, and 2 QPSK symbols on the discrete nonlinear spectrum associated to the fixed eigenvalues {0.3j,0.6j}. Overall, there were 72 bits over a time window of 8ns. Such a large time window can be significantly reduced considering the desired propagation distance and/or improved techniques.
3.1. Digital signal processing
The digital signal processing (DSP) chains implemented at the transmitter and receiver contains all the steps required by a conventional system (e.g., bit mapper, carrier frequency offset, frame synchronization) plus all the steps required for the nonlinear spectrum modulation at the transmitter and the demodulation at the receiver. On the one hand, at the transmitter, the information was mapped independently on the continuous and the discrete part of the nonlinear spectrum. Then, the inverse NFT was performed to obtain from the nonlinear spectrum (that contains the information) the time domain signal to be sent into the fiber. This part was quite challenging, since there is not a procedure supported by an exact mathematical theorem (at least, we are not aware of this). Consequently, we used a procedure, suggested by the single polarization case, whose accuracy was confirmed a posteriori with our numerical simulations. On the other hand, at the receiver, the received signal was used to perform a direct NFT to obtain the nonlinear spectrum. The inverse channel transfer function was applied to remove the channel propagation effects and obtain a noisy version of the transmitted nonlinear spectrum, from which the information sent was retrieved.
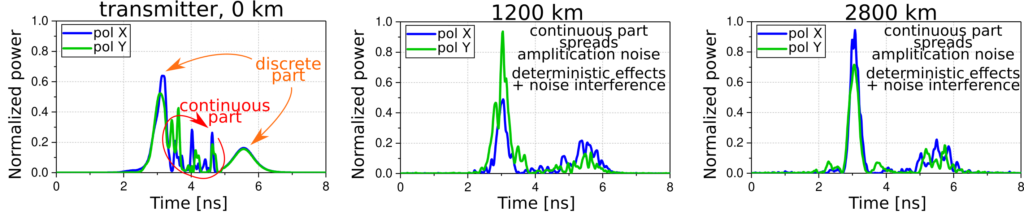
Figure 2: Optical signal at different distances along the fiber (left) transmitter side, digital waveform (middle) 1200 km, (right) 2800 km. Figure adapted from [14].
3.2. Experimental setup
The experimental setup used a 64-GSamples/s arbitrary waveform generator driving the IQ modulator, which encoded the signal into an optical carrier generated by a low-linewidth fiber laser. The link consisted of a recirculating loop based on four 50-km transmission spans with Raman amplified amplification. Loss, dispersion and nonlinear coefficient of the fiber are 0.155 dB/km, 22 ps/nm/km and 0.6 /W/km, respectively. At the receiver side, an 80-GSamples/s digital storage oscilloscope acted as an analog-to-digital converter.
3.3. Transmission performance
The system is investigated at different distances along the fiber. The time domain signal is shown in Fig. 2. A transmission reach of 3200 km was demonstrated with a bit error rate small enough to use hard decision forward error correction codes to correct for the errors. Overall, the net transmission rate was 8.4 Gb/s.
4. Conclusions
Optical fiber communication systems based on the NFT have been recently investigated for their inherent robustness against fiber nonlinearity, aiming at improving the performance of the optical network. In this work, we experimentally demonstrated for the first time the transmission of a signal using the NFT to modulate all the degrees of freedom for NFDM systems available on a single mode fiber, i.e., both polarizations and nonlinear spectra.
5. References
[1] G. P. Agrawal, Fiber-optic communication systems (John Wiley & Sons, 2002).
[2] E. Agrell, M. Karlsson, A. Chraplyvy, D. J. Richardson, P. M. Krummrich, P. Winzer, K. Roberts, J. K. Fischer, S. J. Savory, B. J. Eggleton et al., “Roadmap of optical communications,” Journal of Optics 18, 063002 (2016).
[3] A. Hasegawa and T. Nyu, “Eigenvalue communication,” Journal of Lightwave Technology 11, 395-399 (1993).
[4] M. I. Yousefi and F. R. Kschischang, “Information transmission using the nonlinear Fourier transform”, Parts I-III, IEEE Transactions on Information Theory 60, 4312-4369 (2014).
[5] J. E. Prilepsky, S. A. Derevyanko, K. J. Blow, I. Gabitov, and S. K. Turitsyn, “Nonlinear inverse synthesis and eigenvalue division multiplexing in optical fiber channels,” Physical review letters 113, 013901 (2014).
[6] S. T. Le, J. E. Prilepsky, and S. K. Turitsyn, “Nonlinear inverse synthesis for high spectral efficiency transmission in optical fibers,” Optics Express 22, 26720-26741 (2014).
[7] M. J. Ablowitz and H. Segur, Solitons and the inverse scattering transform, vol. 4 (SIAM, 1981).
[8] M. J. Ablowitz, B. Prinari, and A. D. Trubatch, Discrete and Continuous Nonlinear Schroedinger Systems (Cambridge University Pres, 2004).
[9] S. Civelli, Nonlinear frequency-division multiplexing: theoretical aspects, numerical algorithms, and experimental demonstration, PhD thesis, Scuola Superiore Sant’Anna, Pisa, Italy (2019).
[10] S. K. Turitsyn, J. E. Prilepsky, S. T. Le, S. Wahls, L. L. Frumin, M. Kamalian, and S. A. Derevyanko, “Nonlinear Fourier transform for optical data processing and transmission: advances and perspectives,” Optica 4, 307-322 (2017).
[11] S. T. Le, V. Aref, and H. Buelow, “Nonlinear signal multiplexing for communication beyond the Kerr nonlinearity limit,” Nature Photonics 11, 570 (2017).
[12] A. Maruta and Y. Matsuda, “Polarization division multiplexed optical eigenvalue modulation,” in “2015 International Conference on Photonics in Switching (PS),” (IEEE, 2015), pp. 265-267.
[13] S. Gaiarin, A. M. Perego, E. P. da Silva, F. Da Ros, and D. Zibar, “Experimental demonstration of dual polarization nonlinear frequency division multiplexed optical transmission system,” in “European Conference on Optical Communication 2017 (ECOC),” (2017), p. W.3.C.2.
[14] F. Da Ros, S. Civelli, S. Gaiarin, E. P. da Silva, N. De Renzis, M. Secondini, and D. Zibar, “Dual-polarization NFDM transmission with continuous and discrete spectral modulation,” Journal of Lightwave Technology (2019).